Chapter 8 - Modelling and testing decisional ambidexterity
Laws should only provide a basis for self-fulfilment. Paul Klee
In this first modelling chapter, in the same fashion as described in the beginning of our literature review, we propose to come back to a canonical model that requires to be enhanced by generative processes. James March in his seminal paper had consciously declared the boundaries of his model (March 1991); yet these very same edges are heavily challenged by the evolutions of innovation management which have gone beyond the perimeters of the ambidexterity models relying on the non-mutual conditioning between exploration/exploitation. Generative processes such as design practices taking place for radical innovation, ripple throughout decision-making, collective action, coordination mechanisms and organizations.
Based on the management anomaly specifications and the mirroring requirements needed to design a new model, we propose to synthesize the article published in the European Management Review (Le Masson et al. 2018) (see publication). The developed model allows clarifying the heuristics associated with decisional ambidexterity (Le Glatin, Le Masson, and Weil 2017) (see publication). Furthermore, it gives some grounds on the designing of decisions and to set a new frame for collective action.
We discuss which extensions are made on the traditional assumptions on problem-solving and rational theory of choice thanks to the teachings in design theory. We can then revisit some stimulating constructs previously identified in our literature review discussing the performance of the decision design relating to the innovation potential of attraction and underlying useful methods and heuristics.
All along the modelling effort in the following section, we make several references to the previous detected anomalies. We do so in order to explain how the new model allows gaining new insights. We also refer to the gap-filling between former models and the new as we also tasked ourselves to keep coherence and a sense of continuity when coming from the known to the unknown.
We start by coming back to the original model of (March 1991) with its foundations in problem-solving and choice of alternatives. We extend the canonical framework of decision-making into the unknown with the support of C-K design theory.
Then, we discuss the performance of the decisions designed and made. It invites to think beyond traditional expected utility theories of choice.
The first partial representation of the model is pictured in table gives a comparison with the synthetic model of non-mutual conditioning between exploration and exploitation.
Designing decisions: decisional ambidexterity for organizational metabolism
In the introduction and premises of our literature review (see chapter 1, we presented the trajectory of the agent-based model of James March, creating the construct of exploration and exploitation to sustain organization learning and fighting for supremacy (March 1991). The starting point being problem-based - and consequently decision-making by adding a pinch of uncertainty - allows considering the bounded rationality of agents limited in their daily routines, and requiring exploration, i.e. search-based patterns looking out for overlooked alternatives already present in their decision space.
The issue of the decision creation is rather left aside by only promoting the garbage-can decision model and foolishness as a means to improve the generation of novelty, beyond pure selection issues. Without discarding altogether a potential contribution from foolishness and irrationality, starting from the canonical model of decision theory such as (Wald 1945, 1949)1 where an agent picks up an alternative among those offered to her, consequences $X$ are known depending on the outcome of the states of nature $\Theta$.
The (statistical) decisions ($d:s\in \Theta \rightarrow x\in X$, $d\in D$) are calculated based on costs of consequences ($c:x\in X \rightarrow y\in\mathbb{R}^+$) and the states of nature weighted by degrees of probability $\mu$. The theory predicts the existence of an optimal choice minimizing costs.
Using design theory, such as C-K theory (Hatchuel and Weil 2009), for its generality can be used onto the canonical model $(D,\Theta,c,\mu)$ which can be complemented by statistical learning $L$ drawn from previous experiences and sampling $(D,\Theta,c,\mu,L)$. We also address the issue of simultaneous problem formulation and solving, conceptualized in need-solution pairs (Hippel and Krogh 2016) who encouraged the use of design theory to identify and generate these pairs.
Mobilizing design theory for decision paradigm
The dominant design stemming from the decision problem is the optimum choice in the acknowledged set of choices, beliefs, states of nature and cost function. Using C-K theory gives a starting point formulated by a model of knowledge that can be considered as the state of the art, and the decision broken down into the given environment $\Theta$ and optimal decision maximising expected utility $d_{MEU}$ (minimizing costs). We then have a first branch on the concept space, and a first knowledge sub-space.
Naturally, the Wald’s model gives it own parameters that can be hacked by design. The set of decisions $D$ and the states of nature $\Theta$ can be then re-designed. Generativity, like in the experiment where pigeons generate new action to solve a problem (Epstein et al. 1984; Epstein 1990), will play on the generation of new decisions, as well as altering the states of nature. It differs from trial and error in the way that it deals with novelty, ill-defined problems, by matching stimuli and actual transformation of the behaviour required to deal with (generated) new situation.
In a very simple way, we are interested in managing the operators $D \rightarrow D^{* } $, which generates and reconfigures decisions, and $\Theta \rightarrow \Theta^*$ which integrates new states of nature,
changes the world’s description, semantics and changes the posture of the decision-maker with respect to these states. The cost function $c$, and beliefs $\mu$ will subsequently have to be redefined or simply extended to the new range.
Coming back to the figure show in the literature review (see section), copied below, we push the model beyond the Pareto front. As the operators generate new possibilities, revisiting performance criteria which are the tip of the iceberg of the transformations of $D$ and $\Theta$.

New decision categories
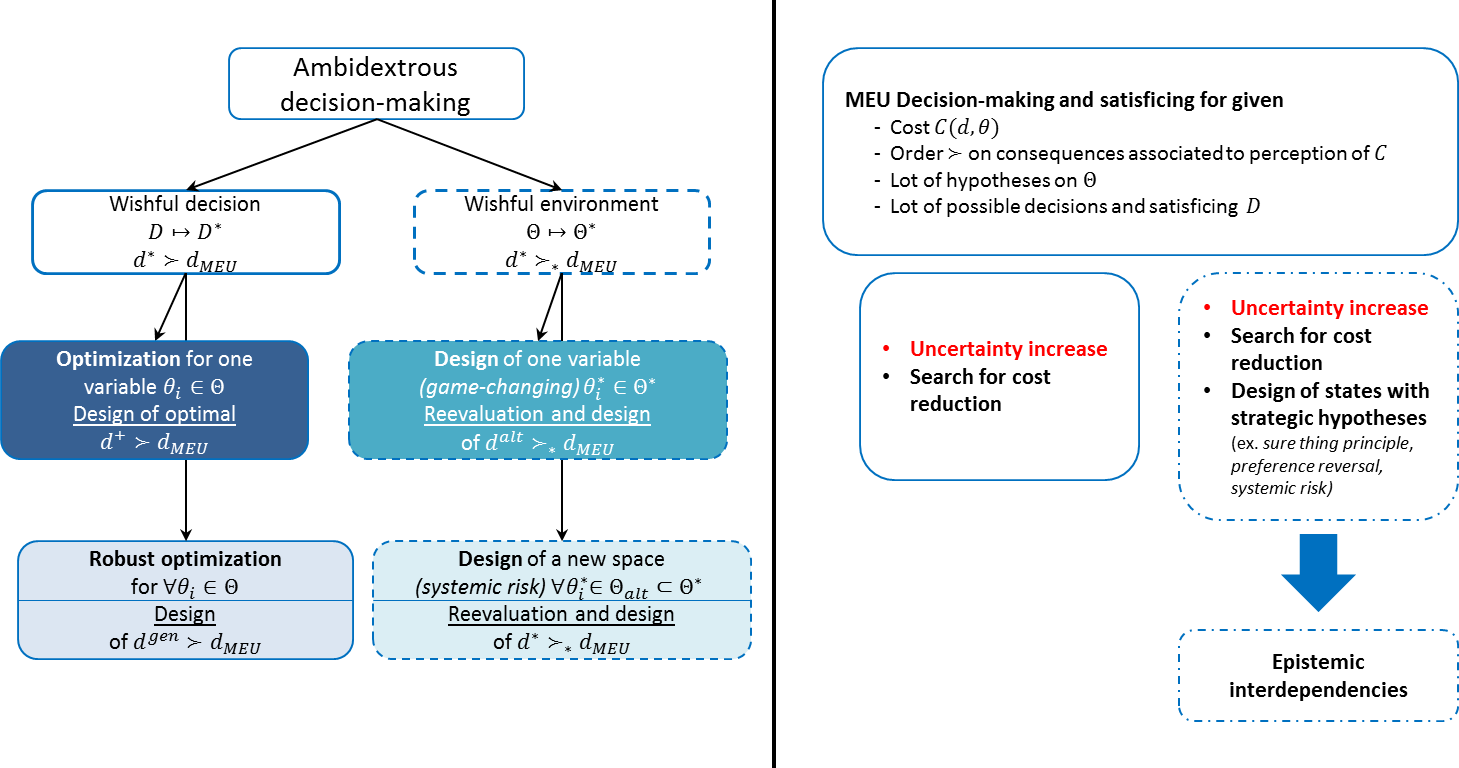
Firstly, beyond the optimum decision $d_{MEU}$, the decision-designer can try to push the optimization even further for a given chosen state of nature $\theta_i \in \Theta$. We have then a **new wishful decision by optimization** ($d_{opt}$). It could be a simple functional improvement added for one feature that could be constrained otherwise by the realization of one outcome in the spectrum of consequences.
Optimizing makes the assumption that a lot of parameters have been identified and locked, so that gap to be explore between what is boundedly known and what is yet to be known is clear. It could be considered as the simplest and predictive form of transitioning between exploration and exploitation.
Secondly, the uncertainty associated to the considered states of nature $\Theta$, the decision-designer can study the envelop of available alternatives $D$ so that he can add a new decision which minimizes costs for all contingencies: new wishful decision by genericity ($d^{gen}$).
In the Business Class seat, we can label some of their decisions aiming at developing a platform for a modular product line. The exploration of existing possibilities (benchmark) and the generation of new alternatives both encompass a new wishful decision by genericity.
We can also argue that when the client program selected the explored product design, the exploitation regime performs a regression towards optimizing as if the preliminary platform design would be robust enough for a full development and uncertainty reduction. Some knowledge areas had indeed not been fully uncovered. So, in a post mortem analysis, we have a better understanding of what could have been managed differently to maintain the exploration and exploitation effort and their mutual conditioning.
Now switching to the design heuristics, instead of leaving $\Theta$ fixated, we can work on redesigning the states of nature. Thirdly, we can try to change a single state of nature in order to force the redesign of decisions. Considering an unknown (i.e. out of the domain) state of nature that may have a devastating impact on consequences can be one way. Or one could simply just slightly shift a not very likely state of nature. The idea of the What If? scenario in Design Thinking methodology addresses this perspective. However, one can also target the most certain knowledge which hides fixation effects; it tackles the sure thing principle (Savage 1954, 21).
Following the same fashion, deliberately reversing preferences can force the design or the concern for an unknown state of nature which may favour the reversal; as discussed in our paper (Le Glatin, Le Masson, and Weil 2017), also in publication.
We are then designing a new wishful decision by best choice hacking ($d^{alt}$). For example, if the decision problem was to choose between known several technologies and associated performance, one could try reversing the order and try to design a situation where it would work.
The Icing Conditions Detection case can be interpreted in that way since considering an unknown safety regulation evolution was to be shaped by the R&T manager to justify the new performance of the technology in the new spectrum.
Exploration effectively relies on exploitation constraints to generate new alternatives. It could be also considered as coming out of the blue, in a serendipitous way, as an externality or as need-solution pair (Hippel and Krogh 2016). But at least, the model allows linking them back to the dominant designed decision, since we can play on the decision space and states of nature.
Finally, we can reproduce systematically all pieces of certain knowledge. By doing so, we explore the full extent of fixation effects considered on knowledge usually requested or made implicit in decision-making. So we end up with a new wishful decision by all choices hacking ($d^{*}$).
In the Design Thinking cases, shifting the concepts in aircraft areas, where BUs are not dealing with the design brief, falls into the category of all choices hacking. Clearly, it highlights that the exploration has gone out of the boundaries of what classical search-based model would have delivered. Such hacking insists on the fact that exploitation won’t be conducted nor balanced by ignoring the new created interplay. Frontier between product designs can be totally re-discussed to shape the new environment (e.g. lower deck, integration between equipment in galley area, passengers loading their luggage, etc.).
Knowledge value
The different decisions categories, by simply relying on Wald’s canonical decision model, show the extension $D$ and $\Theta$ spaces. The transformation operated by design theory comes with consequences on the value $c$, beliefs $\mu$ and learning $L$. These are redefined by composition of $D \rightarrow D^{* }$ and/or $\Theta \rightarrow \Theta^{* }$.
The most stimulating feature from a standard statistical probability view is that adding a new decision, or new state of nature, flattens existing probability distributions. In other words, we increase global uncertainty. And we do it so that it is even more accentuated that it could perturb a search-based model since we are extending the spaces we are relying on. From a rational choice theory, it is, of course, unacceptable but the operators in between the old and the new spaces take in the possibility of design, it is not an externality.
In the Icing Conditions Detection project, when they reversed their preferences for a highly uncertain technology, they opened a new environment to be shaped. The potential risk was reallocated, raising uncertainties but also made former alternatives less interesting despite being more certain in a different setting.
Learning can be organized for such purpose. Seen from the development engineering department, the prototype tested on aircraft is not to be considered as a traditional exploitation. Instead, it should be seen as an exploitation exploration where the unfinished engineering work offers the opportunity to acknowledge and reconfigure engineering rules around the new technology and system.
We consequently endogenize the unknown by design. Not only are we are building up awareness but also we are anticipating it by systematically designing and prospectively managing unknown decisions and states of nature. We are in line with the idea of bringing vigilance (Oury and Schmidt 1983), opportunism (Lumineau and Verbeke 2016), reliability (Sutcliffe and Christianson 2012) to the front seat, by turning the decision-maker into a decision-designer. The underlying assumptions have been weakened to leave room for design theory to unveil its potential on its sister theory.
The concept of phronesis (Nonaka, Hirose, and Takeda 2016), which we discussed in the literature review, could be then further substantiated with the way a manager makes and design decisions. It is a means of organizing collective action: creating simple coordination mechanisms around certain knowledge that can tweaked collectively by stakeholders, mobilizing (silent) designers around problems that can be systematically ill-defined by themselves, and simply overseeing the course of action with other reference points given by the decisional mapping.
In the BC class seat platform project, the early stages of concept selection and generation with BU stakeholders were an actual case of blending the exploration with the exploitation constraints. However, this effort was biased when the project was transferred to program management as if fit for development. Instead, it could have been the occasion to continue exploitation knowing and managing learning for a continuing and parallel exploration. This awareness is however only realized in the aftermath and not along the transition nor the exploitation project management.
Performance of decision design
The described approach of simply applying a generativity theory to a foundational canonical model puts the emphasis on the transformation operators rather than on the dichotomy of exploration and exploitation regimes. These operators offer a systematic way of exploring given exploitation references. The dichotomy and non-mutual conditioning are left aside by a constant articulation of interdependencies of exploration and exploitation. So, it is not the set of elements and their nature that counts, but rather the relationship engaged between them that is to be managed. In that regard, we move beyond duality of the regimes (Farjoun 2010).
Beyond the fit: moving and designing target
The paradoxes of opposing two competing objectives becomes rather secondary or even transparent, by adopting the design and elucidation of interdependencies between decisions and states of nature. All the ties justifying exploration can be derived from exploitation, and conversely the exploitation can be justified by a reference enlarged by exploitation.
The constant generative search is rooted in exploitation, and exploitation is inversely valued through exploration. The pattern is similar to the novelty-search algorithm (Nguyen, Yosinski, and Clune 2015; Cully et al. 2015) designed for robots to improve their resilience, but we improve such heuristics by considering that the problem is also re-formulated, as if the underlying algebra was reconfigured.
For instance, not only has the robot a performance objective (reaching a given point in space), the novelty-search algorithm will generate new movements in two dimensions without knowing the terrain. But, it will only operate with the possible actuators available and their performance range. It is also crucial to reconsider the actuators framing the range and nature of alternatives. This is what we achieve with our operators.
Conditioning exploration by exploitation, can be considered actually quite natural but let us remember that numerous design and creativity methods encourage to liberate constraints and be careful with brief formulation. Thinking out of the box also requires starting by defining the box itself.
In the icing conditions detection project, opposing the technology alternatives imposes to value them against a given system, integration and regulations. Reversing the preferences, encourages to reconfigure the value framework: new system, new integration constraints and new regulations. The problem reformulation is built upon an exploitation constraint and target on the move. Consequently, a fraction of the project management is driven towards ensuring the target is managed to satisfy preferences reversal.
Overcoming biases and fixation effects
The performance of exploration will be seen through the generativity of the design practices. These will be valued relatively to reference points which can be previously generated decisions or potential decisions. But as the end game is to be able to decide and organize collective action for these, it would be even more practical to set the reference on exploration points.
We have discussed exploitation and weak exploration natural reliability, path dependency, can not only be biased due to bounded rationality but also can be fixated due to lack of understanding of environment awareness, system thinking and organizational design.
Newly generated concepts may be indeed challenging epistemic interdependencies which will have to be carefully managed when these are revealed by directly concerned decision-makers. It is then preferable to have them actively dealing with the (re)-design practice of these interdependencies and their rationality that was contextually established and fixated.
As James March partly addressed it (see quotation below (March 2006, 209)), he gave a few hints on how the produce of exploration, be it foolish or not, would eventually become rational and exploited could be used as a basis for exploration. We believe that our model allows elucidating this mutual conditioning and how to exploit it for exploration and vice-versa. This complement to the separation between exploration and exploitation had been omitted in the original model (March 1991) as noted in our literature review. It underlines the natural interaction between what makes exploration and exploitation. However, it doesn’t imply necessarily a continuum nor orthogonality, but rather multiple relationships to be surfaced and managed.
It is argued that the link between rationality and conventional knowledge keeps rational technologies reliable but inhibits creative imagination. This characterization seems plausible, but it probably underestimates the potential contribution of rational technologies to foolishness and radical visions.
In the Design Thinking cases, an external observer, unfamiliar with the history of aircraft cabin equipment and stringent standards & regulations, could easily consider product designs, interfaces and usage totally foolish. Different value networks taken from other user experience (passenger, cabin crew) will confront to rationally developed products and services.
Anchoring the exploration to exploitation provides a playground to relieve constraints faced by dominant designs, promoting new interactions with users, or even hacking altogether how things are done and envision a new environment (e.g. lower deck, passenger boarding). However, the learning associated with the defixation is to be further explained as it unlocks several interdependencies that are not self-evident when just showcasing concepts or prototypes.
The performance is discussed in different ways and through action engaged in the decision-design process. Adaption model is left close enough to optimizing decision and richer exploration can be achieved by challenging beliefs, preferences order and states of nature. Interactions can be managed around these parameters. And the encapsulation can be tracked and positioned with respect to learning challenges.
Finally, not only the distance is generated away from a dominant design, fixation points and ingrained interdependencies, but it is also key to enable the constant transformational dialog between these two.
Performance of decision design is then substantiated through the heuristics presented earlier and the necessity of interacting through them. It will target multiple parameters in engineering design and constraints.
Model synthesis
Below, the figure 2 represents, with C-K formalism, the different designed decision categories and the knowledge used. We specify the different wishful decisions and the enabling knowledge hacked to design new decisions and new states of nature. Following customs in C-K theory, the dominant design is left on the left of the concept tree where we have put the wishful decision by optimization ($d_{opt}$). A variation to the optimization can be then to design by considering a wishful decision by genericity ($d^{gen}$). It considers as many states of nature possible by defining an envelop of consequences that the decision should be ready to address. Then, hacking the states of nature, opens a new branch with two new designed decisions categories: wishful decision by best choice hacking and all choices hacking. The first tackles what could be the dominant, what is more obvious, the sure thing principle. The second shifts the decision problem in a new environment.
The table [table:modelADMtab], brings the comparison between the newly designed model of mutual conditioning of exploration/exploitation and the former derived from the literature. Several items have to be further specified given the chosen descriptors used for the anomaly detection. We have discussed the fixation effects and necessary anchoring to exploitation parameters facilitating the management of exploration. The mutual conditioning between exploration and exploitation will channel learning, dealing with interdependencies. Therefore, it will also require looking beyond the cognitive dimension of decision-designing. Organization design, the mirroring dynamic as well as action modes organizing decisional ambidexterity will have to be taken into account to fully cover the anomalies identified with all descriptors. These incomplete model features presented in the following table will be discussed in the [following chapter] (https://mleglatin.github.io/phd/part4/chapter9/). The organizational metabolism can then be discussed in more detail to sustain organizational change and learning.
| Model descriptors | Non-mutual conditioning | Mutual conditioning extended model |
|---|---|---|
| Model of coordination and collective action | 1. Not necessarily on the same continuum, exploration and exploitation call for two dissociate action regimes. 2. Balancing is left as a paradox at different levels of analysis: structure (centralization, distribution), time and individuals. |
1. Exploration and exploitation are mutually used to support extended decision-making. 2. The balancing paradox is dealt by design operators valuing mutual benefits of exploration and exploitation. It is organized through interactive decision-design practices. (To be completed. See next chapter) |
| Generative processes | 3. The nature of generative processes supporting exploration appears quite free, random and sometimes even foolishness-based. 3. Generativity of the product development may not be sustained by (temporary) organizations (floating issue). 4. The performance and reference are light structured: reduced to a selection issue or sometimes to complex interactionist phenomenon. |
3. Generative processes target the exploration/exploitation bone of contention and associated decision-making. 4. Generativity is articulated around design fixations and interdependencies for better interactive value management with other (silent) decision-designer. 5. Performance is repositioned on the transformative feature of decision-design where its criteria are redefined. (To be completed. See next chapter) |
| Environment cognition | 6. One-way interaction: Environment to Organization. 7. The environment structures the response, nature and distribution of generative processes. 8. The environment is used to augment the product development requirements. |
6. The environment is managed through decision-design. 7. The decision-design addresses environment-induced fixations. 8. The environment awareness developed through decision-design targets also (potential) interdependencies and future exploitation features. (To be completed. See next chapter) |
| Organization design | 9. Organization design is pre-conceived or uncontrolled. 10. Organization design creates gaps for managing generative processes and the dynamics of their organizational ties. |
See next chapter |
Chapter synthesis: designing decisions for cognitive ambidexterity
We have used the requirements listed in the previous chapter after detecting and specifying the anomalies in several cases. We have then proposed to start anew by coming back to the beginning of our literature review.
The canonical model of decision theory (Wald 1949, 1945) is mobilized to consider the problems-solving with uncertainty described in the seminal paper (March 1991). As we had repeatedly tested the edges of the literature models of non-mutual conditioning between exploration and exploitation, we have used the teachings of design theory to extend decision theory into the unknown.
It allowed specifying different decision categories and heuristics playing with decision problem parameters and formulation. The model proposed an extended risk management as the uncertainty is increased by design but at the same time uses exploitation core specified by fixation effects, biases of bounded rationality and interdependencies to ground exploration and manage its generativity and value.
We have also made reference to the previous anomalies and made sense of them with the help of the decision ambidexterity. They fall into several designed decision categories in the unknown and they let clarifying what has been missed or what was in the blind spot of models of ambidexterity.
The following chapter complements the gaps left in the model’s description as we had specified several organizational descriptors to detect the anomalies. We will define further decisional ambidexterity with our concern for strategic management and organizational learning and change.
References
Cully, Antoine, Jeff Clune, Danesh Tarapore, and Jean-Baptiste Mouret. 2015. “Robots that can adapt like animals.” Nature 521 (7553): 503–7. https://doi.org/10.1038/nature14422.
Epstein, R, C E Kirshnit, R P Lanza, and L C Rubin. 1984. “Insight in the pigeon: antecedents and determinants of an intelligent performance.” Nature 308 (5954): 61–62. https://doi.org/10.1038/308061a0.
Epstein, Robert. 1990. “Generativity Theory and Creativity.” In Theories of Creativity, edited by Mark A. Runco and Robert S. Albert, 116–40. Sage Publications.
Farjoun, Moshe. 2010. “Beyond dualism: Stability and change as a duality.” Academy of Management Review 35 (2): 202–25. https://doi.org/10.5465/AMR.2010.48463331.
Fourcade, Marion, and Rakesh Khurana. 2013. “From social control to financial economics: the linked ecologies of economics and business in twentieth century America.” Theory and Society 42 (2): 121–59. https://doi.org/10.1007/s11186-012-9187-3.
Giocoli, Nicola. 2013. “From Wald to Savage: Homo Economicus Becomes a Bayesian Statistician.” Journal of the History of the Behavioral Sciences 49 (1): 63–95. https://doi.org/10.1002/jhbs.21579.
Hatchuel, Armand, and Benoit Weil. 2009. “C-K design theory: An advanced formulation.” Research in Engineering Design 19 (4): 181–92. https://doi.org/10.1007/s00163-008-0043-4.
Hippel, Eric von, and Georg von Krogh. 2016. “CROSSROADS—Identifying Viable ‘Need–Solution Pairs’: Problem Solving Without Problem Formulation.” Organization Science 27 (1): 207–21. https://doi.org/doi:10.1287/orsc.2015.1023.
Le Glatin, Mario, Pascal Le Masson, and Benoît Weil. 2017. “Generative action and preference reversal in exploratory project management.” CERN IdeaSquare Journal of Experimental Innovation 1 (2): 39–46. https://doi.org/10.5170/cij.2017.539.
Le Masson, Pascal, Armand Hatchuel, Mario Le Glatin, and Benoit Weil. 2018. “Designing Decisions in the Unknown: A Generative Model.” European Management Review. https://doi.org/10.1111/emre.12289.
Lumineau, Fabrice, and Alain Verbeke. 2016. “Let’s give opportunism the proper back seat.” Academy of Management Review 41 (4): 739–41. https://doi.org/10.5465/amr.2015.0410.
March, James G. 1991. “Exploration and exploitation in organizational learning.” Organization Science 2: 71–87.
March, James G. 2006. “Rationality, foolishness, and adaptive intelligence.” Strategic Management Journal 27 (3): 201–14. https://doi.org/10.1002/smj.515.
Nguyen, AM, J Yosinski, and J Clune. 2015. “Innovation engines: Automated creativity and improved stochastic optimization via deep learning.” Proceedings of the 2015 on Genetic. http://dl.acm.org/citation.cfm?id=2754703.
Nonaka, Ikujiro, Ayano Hirose, and Yusaku Takeda. 2016. “‘Meso’-Foundations of Dynamic Capabilities: Team-Level Synthesis and Distributed Leadership as the Source of Dynamic Creativity.” Global Strategy Journal 6 (3): 168–82. https://doi.org/10.1002/gsj.1125.
Oury, Jean-Marc, and Christian Schmidt. 1983. Economie politique de la vigilance. Paris: Calmann-Lévy.
Raiffa, H. 1968. Decision Analysis: Introductory Lectures on Choices Under Uncertainty. Mcgraw-Hill College.
Savage, Leonard. 1954. The foundations of statistics. 2. New York.
Sutcliffe, Kathleen M., and Marlys K. Christianson. 2012. “Managing the Unexpected.” In The Oxford Handbook of Positive Organizational Scholarship. https://doi.org/10.1093/oxfordhb/9780199734610.013.0064.
Wald, Abraham. 1945. “Statistical Decision Functions Which Minimize the Maximum Risk.” The Annals of Mathematics 46 (2): 265. https://doi.org/10.2307/1969022.
———. 1949. “Statistical Decision Functions.” Annals of Mathematical Statistics 20 (2): 165–205. https://doi.org/10.1214/aoms/1177730030.
-
It is considered as foundational for decision-theory, as (Savage 1954) derived his model from it, as well as the management variant of (Raiffa 1968). In (Giocoli 2013), the model’s trajectory over time is drawn showing the structuring role of Bayesian probability theory, as well as its diffusion in management education (Fourcade and Khurana 2013). ↩︎